 |
Interactive Tutorials
Electromagnetic Wave Propagation
Electromagnetic waves can be generated by a variety of methods, such as a discharging spark or by an oscillating molecular dipole. Visible light is a commonly studied form of electromagnetic radiation, and exhibits oscillating electric and magnetic fields whose amplitudes and directions are represented by vectors that undulate in phase as sinusoidal waves in two mutually perpendicular (orthogonal) planes. This tutorial explores propagation of a virtual electromagnetic wave and considers the orientation of the magnetic and electric field vectors.
To rotate the wave model, click and drag anywhere within the window.
The tutorial initializes with an electromagnetic wave being generated by the discharging spark from a virtual capacitor. The spark current oscillates at a frequency characteristic of the circuit, and the resulting electromagnetic disturbance is propagated with the electric (E) and magnetic (B) field vectors vibrating perpendicular to each other and to the direction of propagation (Z). The wavelength emitted by the virtual capacitor discharge can be altered (within the visible light range) by using the Wavelength slider.
Before discussing the phenomenon of anisotropy further, a basic review of several physical optics principles, necessary to subsequent discussions, is required. As previously mentioned, visible light is a form of electromagnetic wave. If a capacitor is charged (Figure 1) and a spark is discharged through the two electrodes, the current induced by the spark flows down for a short time, slows down, but because of the inductance of the circuit, flows back upwards, recharging the capacitor again.
The propagation of an electromagnetic wave, which has been generated by a discharging capacitor or an oscillating molecular dipole, is illustrated by Figure 1. The spark current oscillates at a frequency (n), which is a characteristic of the circuit. The electromagnetic disturbance that results is propagated with the electronic (E) and magnetic (B) vectors vibrating perpendicularly to each other and also to the direction of propagation (Z). The frequency, n, is determined by the oscillator, while the wavelength is determined by the oscillation frequency divided by the velocity of the wave.
As the current oscillates up and down in the spark gap, at the characteristic circuit frequency (n), a magnetic field is created that oscillates in a horizontal plane. The changing magnetic field, in turn, induces an electric field so that a series of electrical and magnetic oscillations combine to produce a formation that propagates as an electromagnetic wave.
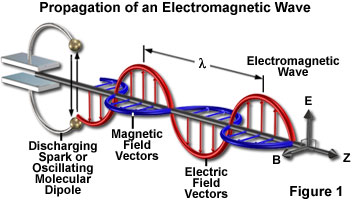
The electric field in an electromagnetic wave vibrates with its vectorial force growing stronger and then weaker, pointing in one direction, and then in the other direction, alternating in a sinusoidal pattern (Figure 1). At the same frequency, the magnetic field oscillates perpendicular to the electric field. The electric and magnetic vectors, reflecting the amplitude and the vibration directions of the two waves, are oriented perpendicular to each other and to the direction of wave propagation.
The velocity of the resulting electromagnetic wave can be deduced from the relationships defining the electric and magnetic field interactions. Maxwell's equations prove that velocity equals the speed of light in a vacuum (c; equal to 300,000 kilometers per second) divided by the square root of the dielectric constant (x) of the medium times the magnetic permeability (m) of the medium. Thus,
|
(1) |
For most materials that occur in living cells (some of which are non-conducting), the magnetic permeability is equal to a value of unity, so that:
|
(2) |
Empirically, the velocity of light is known to be inversely proportional to the refractive index (n) of the material through which it propagates, therefore:
|
u = c/n |
(3) |
From equations (2) and (3), the conclusion can be drawn that refractive index is equal to the square root of the dielectric constant of that material if the measurements are made at the same frequency:
|
(4) |
Equation (4) reveals that optical measurements are, in fact, measurements of the electrical properties of the material. The dielectric properties, in turn, directly reflect the spatial three-dimensional arrangement of atoms and molecules that define the structure of a substance.
The vector describing the interaction between an electromagnetic field and a substance lies in the same direction as the electric vector. This is true regardless of whether the electric or magnetic vectors are considered, because what matters is the effect of the electric or magnetic fields on the electrons in the material medium (the magnetic field affects those electrons that move in a plane perpendicular to the magnetic field).
Contributing Authors
Kenneth R. Spring - Scientific Consultant, Lusby, Maryland, 20657.
Shinya Inoué - Marine Biological Laboratory, 7 MBL Street, Woods Hole, Massachusetts, 02543.
Brian O. Flynn, Robert T. Sutter, and Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
BACK TO POLARIZED LIGHT MICROSCOPY
Questions or comments? Send us an email.
© 1998-2022 by Michael W. Davidson and The Florida State University. All Rights Reserved. No images, graphics, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners.
This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the
National High Magnetic Field Laboratory.
Last modification: Thursday, May 19, 2016 at 03:36 PM
Access Count Since April 25, 2001: 233180
For more information on microscope manufacturers,
use the buttons below to navigate to their websites:
