The boundaries of features and structural details in an image are usually defined by changes in brightness or color. Locating these edges so that they can be accurately measured has been an active area of development in image processing. In addition, there is considerable evidence that the steps and edges are key components of a scene selected by human visual processes, and that either extracting them from an image (forming a “sketch” of the scene) or sharpening their appearance assists viewers.

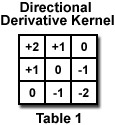
The Laplacian sharpening or unsharp mask filters shown above increase the contrast at steps and edges, but are also sensitive to noise. These operations are mathematically a second derivative of brightness. A first derivative of brightness can be calculated with a kernel such as the one in Table 1 that calculates the difference between neighbors at the upper left and lower right. Because it can produce either positive or negative results, an offset value of 128 (medium gray) is added to the result for display. Eight similar kernels can be formed by rotating the values in 45 degree steps to calculate the derivative in various directions, as shown in the Directional Derivatives interactive tutorial.

	Interactive Tutorial
Directional Derivatives Explore the effect of applying the eight directional derivatives to a color or monochrome image.

The derivative operation is often called an embossing filter because of the appearance it creates. In the example, the RGB color channels are processed individually. Steps and edges oriented perpendicular to the direction of the derivative are enhanced, but those parallel to it disappear.

If the directional derivative is thought of as a vector, two perpendicular derivatives can be combined to calculate the magnitude of the brightness gradient independent of its orientation. This is the widely used Sobel gradient operator, which applies the kernel in the vertical and horizontal directions to each pixel using brightness rather than color values, and then takes the square root of the squares of the magnitude of the two results to form a new image. In the Sobel Gradient Operator interactive tutorial, the process is applied to the brightness values only.

	Interactive Tutorial
Sobel Gradient Operator Apply the Sobel gradient operator to color and monochrome images.

There are many other functions that may be used to mark steps and edges. For example, the statistical standard deviation or variance of the pixels in a small neighborhood rises abruptly at boundaries. For a color image, the range, or maximum vector difference between any pair of neighbor pixels, is often useful. The Statistical Filters interactive tutorial illustrates these techniques.

	Interactive Tutorial
Statistical Filters Apply variance, standard deviation, and range filters to color and monochrome images.

A different approach to enhancing the visibility of steps and making their location more precise operates by transforming gradual changes in brightness that extend over several pixels into an abrupt change. A useful analogy is the buttes and mesas in the American southwest, which rise with sheer walls from the desert floor. Erosion causes these walls to slump. In the same way, the finite size of pixels in the camera averages brightness values from both sides of a step, producing an intermediate value. Reversing this effect can restore the step sharpness as shown in the Kuwahara Filter interactive tutorial. Called a maximum likelihood technique, this procedure compares the statistical properties of neighborhoods around each pixel and assigns to the pixel the average value of the neighborhood that it is most like.

	Interactive Tutorial
Kuwahara Filter Explore the effect of applying a Kuwahara filter to color and monochrome images.

---

BACK TO INTRODUCTION TO DIGITAL IMAGE PROCESSING AND ANALYSIS

BACK TO MICROSCOPY PRIMER HOME

Questions or comments? Send us an email.

© 1998-2009 by Michael W. Davidson, John Russ, Olympus America Inc., and The Florida State University. All Rights Reserved. No images, graphics, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners.

This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the
National High Magnetic Field Laboratory.

Last modification: Thursday, Sep 20, 2018 at 10:14 AM

Access Count Since July 20, 2006: 7555

For more information on microscope manufacturers,
use the buttons below to navigate to their websites: