 |
Interactive Tutorials
Simple Bi-Convex Thin Lenses
A simple thin lens has two focal planes that are defined by the geometry of the lens and the relationship between the lens and the focused image. Light rays passing through the lens will intersect and are physically combined at the focal plane, while extensions of the rays passing through the lens will intersect with the rays emerging from the lens at the principal plane. The focal length of a lens is defined as the distance between the principal plane and the focal plane, and every lens has a set of these planes on each side (front and rear). This interactive tutorial explores how changes to focal length and object size affect the size and position of the image formed by a simple thin lens.
The tutorial initializes with a simple thin bi-convex lens positioned to the right of a gray arrow termed the Object. Light rays from the object are focused by the lens to form the Image on the image side of the lens (the right-hand side). The heights of the object and image are denoted by the variables H(1) and H(2), respectively, and the division of the latter by the former produces the lens magnification (M). The distance between the lens and the object is denoted by the variable a, while the corresponding distance to the image is represented by the variable b. Because the lens is symmetrical, the object-side and image-side focal lengths are equal (represented by the variable f). The focal length values can be simultaneously altered by adjusting the Focal Length slider between a range of 45 to 66 millimeters. In addition, the Object Height slider can be utilized to change this value within a range of 24 to 74 millimeters. The thin lens equation is also solved in real time beneath the object as the sliders are translated. Visitors should adjust both the image height and the lens focal length and observe the resulting effects on the image size and position.
Traces of light rays passing through a simple bi-convex thin glass lens are presented in Figure 1, along with the other important geometric parameters necessary in forming a focused image by the rays. The focal points of the lens are denoted by the variable F, and there are two separate focal points, one in front of the lens (on the left-hand side of Figure 1) and one behind the lens (on the right). The principal planes of the lens are denoted by dashed lines, and the distance between each principal plane and its respective focal point represents the focal length (f). Because the bi-convex lens illustrated in Figure 1 is symmetrical, the principal planes are located equal distances from the lens surfaces, and the front and rear focal lengths are also equal.
The object (or specimen) being imaged by the lens is positioned in the object plane to the left of the lens and is represented by a red arrow that travels upward from the optical axis, which passes through the center of the lens, perpendicular to the principal planes. Ray traces through the lens (yellow arrows) emanate from the object and proceed from left to right through the lens for form a magnified real image (inverted red arrow) in the image plane on the right-hand side of the lens. The distance between the front principal plane of the lens and the specimen is known as the object distance, and is represented by the variable a in Figure 1. In a similar manner, the distance from the rear principal plane to the image (the variable b in Figure 1) is termed the image distance. These parameters are the fundamental elements defining the geometrical optics of a simple lens and can be used to calculate important properties of the lens, including focal length and magnification factor.
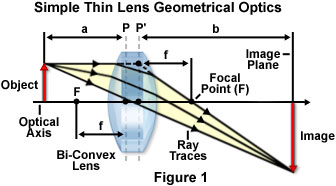
Lenses can be either positive or negative depending upon whether they cause light rays passing through to converge into a single focal point, or diverge outward from the optical axis and into space. Positive lenses (illustrated in Figure 1) converge incident light rays that are parallel to the optical axis and focus them at the focal plane to form a real image. In general, positive lenses have one or two convex surfaces and are thicker in the middle than at the edges. A characteristic of positive lenses is that they magnify objects when they are placed between the object and the human eye. In contrast, negative lenses diverge parallel incident light rays and form a virtual image by extending traces of the light rays passing through the lens to a focal point behind the lens. Negative lenses have at least one concave surface and are thinner in the middle than at the edges. When a negative lens is placed between an object and the eye, it does not form a real image, but reduces (or demagnifies) the apparent size of the object by forming a virtual image.
Contributing Authors
Matthew J. Parry-Hill and Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
BACK TO LENSES AND GEOMETRICAL OPTICS
Questions or comments? Send us an email.
© 1998-2022 by Michael W. Davidson and The Florida State University. All Rights Reserved. No images, graphics, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners.
This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the
National High Magnetic Field Laboratory.
Last modification: Thursday, Sep 20, 2018 at 07:55 AM
Access Count Since August 20, 2002: 101451
For more information on microscope manufacturers,
use the buttons below to navigate to their websites:
