Interactive Tutorials
JPEG Image Compression
The JPEG lossy image compression standard is currently in worldwide use, and is becoming a critical element in the storage of digital images captured with the optical microscope. This interactive tutorial explores compression of digital images with the JPEG algorithm, and how the lossy storage mechanism affects file size and the final image appearance.
The tutorial initializes with a randomly selected specimen image appearing in the left-hand window entitled Specimen Image. Each specimen name includes, in parentheses, an abbreviation designating the contrast mechanism employed in obtaining the image. The following nomenclature is used: (FL), fluorescence; (BF), brightfield; (DF), darkfield; (PC), phase contrast; (DIC), differential interference contrast (Nomarski); (HMC), Hoffman modulation contrast; and (POL), polarized light. Visitors will note that specimens captured using the various techniques available in optical microscopy behave differently during image processing in the tutorial.
Positioned to the right of the Specimen Image window is a JPEG Compressed Image window that displays the captured image at a variety of compression levels, which are adjustable with the Image Compression slider. To operate the tutorial, select an image from the Choose A Specimen pull-down menu, and vary the image compression ratio with the Image Compression slider. The ratio of original image file size to that of the compressed file is presented directly above the slider. By default, the tutorial performs JPEG compression on color images. When the Grayscale Image checkbox is selected, a grayscale version of the image will be loaded into the tutorial and the compression algorithm will be performed on the grayscale image. To view the differences between the compressed and original image, activate the Difference Image radio button. The root-mean-square (RMS) error in compression and the JPEG quality factor are provided in a box below the JPEG Compressed Image window.
The JPEG (Joint Photographic Experts Group) image compression standard has become an important tool in the creation and manipulation of digital images. The primary algorithm underlying this standard is executed in several stages. In the first stage, the image is converted from RGB format to a video-based encoding format in which the grayscale (luminance) and color (chrominance) information are separated. Such a distribution is desirable because grayscale information contributes more to perceptual image quality than does color information, due to the fact that the human eye uses grayscale information to detect boundaries. Color information can be dispersed across boundaries without noticeable loss of image quality. Thus, from a visual standpoint, it is acceptable to discard more of the color information than grayscale information, allowing for a greater compression of digital images.
In the second stage, the luminance and chrominance information are each transformed from the spatial domain into the frequency domain. This process consists of dividing the luminance and chrominance information into square (typically 8 x 8) blocks and applying a two-dimensional Discrete Cosine Transform (DCT) to each block. The cosine transform converts each block of spatial information into an efficient frequency space representation that is better suited for compression. Specifically, the transform produces an array of coefficients for real-valued basis functions that represent each block of data in frequency space. The magnitude of the DCT coefficients exhibits a distinct pattern within the array, where transform coefficients corresponding to the lowest frequency basis functions usually have the highest magnitude and are the most perceptually significant. Similarly, cosine transform coefficients corresponding to the highest frequency basis functions usually have the lowest magnitude and are the least perceptually significant.
In the third stage, each block of DCT coefficients is subjected to a process of quantization, wherein grayscale and color information are discarded. Each cosine transform coefficient is divided by its corresponding element in a scaled quantization matrix, and the resulting numerical value is rounded. The default quantization matrices for luminance and chrominance are specified in the JPEG standard, and were designed in accordance with a model of human perception. The scale factor of the quantization matrix directly affects the amount of image compression, and the lossy quality of JPEG compression arises as a direct result of this quantization process. Quantizing the array of cosine transform coefficients is designed to eliminate the influence of less perceptually significant basis functions. The transform coefficients corresponding to these less significant basis functions are typically very small to begin with, and the quantization process reduces them to zeros in the resulting quantized coefficient array. As a result, the array of quantized DCT coefficients will contain a large number of zeros, a factor that is employed in the next stage to deliver significant data compression.
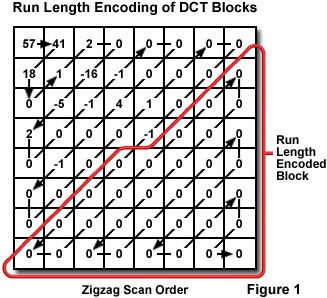
In the fourth stage, a process of run-length encoding is applied to each block of quantized cosine transform coefficients. A zigzag pattern is employed in the run-length encoding scheme to exploit the number of consecutive zeros that occur in each block. The zigzag pattern progresses from low-frequency to high-frequency terms. Because the high-frequency terms are the ones most likely to be eliminated in the quantization stage, any run-length encoded block will typically contain at least one large run of zeros at the end. Thus, the amount of space required to represent each block can be substantially reduced by representing a run of zeros as (0, n), where n is the number of zeros occurring in the run. The process of run length encoding of an 8 x 8 DCT block is illustrated in Figure 1. In the fifth and final stage, the resulting data may be further compressed through a loss-less process of Huffman coding. The resulting compressed data may then be written to the computer hard drive in a file for efficient storage and transfer.
In the tutorial, as the Image Compression slider is moved to the right, the compression ratio of the original image to the compressed image is irregularly increased. The compression ratio is dependent upon the characteristics of the image selected, but these ratios will typically range between 1.1 : 1 to 50 : 1. The JPEG quality factor is a number between 0 and 100 that associates a numerical value with a particular compression level. As the quality factor is decreased from 100, image compression improves, but the quality of the resulting image is significantly reduced. As the Image Compression slider is moved to the right (increasing the compression ratio), additional low-frequency luminance information is discarded and image detail is lost. At the highest compression ratios, 8 x 8 blocking artifacts occur, which mask many of the image features. The consequences of high compression can be seen quantitatively by observing the RMS error, which consists of the sum of the per-pixel intensity differences between the original image and the compressed image. As the RMS error increases, the amount of difference between the original and compressed images also increases.
Compression of images by the JPEG algorithm should be limited to those intended strictly for visual display, such as presentation in Web pages or distributed in portable document format (PDF). Digital images captured in the microscope that are destined for serious scientific scrutiny with regard to dimensions, positions, intensities, or colors of features should never be subjected to lossy compression before analysis. Cameras utilized in scientific or forensic work should have any lossy compression options turned off. It is not possible to examine a compressed image and determine what has been lost, and the losses are distributed very nonuniformly throughout the image, depending upon the amount of local detail.
Contributing Authors
Kenneth R. Spring - Scientific Consultant, Lusby, Maryland, 20657.
John C. Russ - Materials Science and Engineering Department, North Carolina State University, Raleigh, North Carolina, 27695.
Matthew J. Parry-Hill and Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
BACK TO DIGITAL IMAGE PROCESSING TUTORIALS
