Enhancing the overall sharpness of a digital image often has the effect of revealing fine details that cannot be clearly discerned in the original. The unsharp mask filter algorithm is an extremely versatile sharpening tool that improves the definition of fine detail by removing low-frequency spatial information from the original image.

Adjacent to the Specimen Image window is a Filtered Image window that displays the results of applying the unsharp mask filter algorithm to the original image. To operate the tutorial, select an image from the Choose A Specimen pull-down menu, and adjust the Standard Deviation and Weighting Value sliders until the image appears sharper with enhanced detail.

The unsharp mask filter algorithm involves subtraction of an unsharp mask from the specimen image. An unsharp mask is simply a blurred image that is produced by spatially filtering the specimen image with a Gaussian low-pass filter. This filter can be considered as a convolution operation on an image with a kernel mask that is a two-dimensional Gaussian function (g(x,y); as defined in Equation 1):

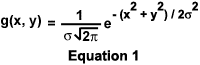
The size of the Gaussian kernel mask is a function of the parameter s, and the size of the kernel mask determines the range of frequencies that are removed by the Gaussian filter. In the tutorial, the Standard Deviation slider determines the value of s in pixels. In general, increasing the size of the kernel mask causes the Gaussian filter to remove a greater number of spatial frequencies from the unsharp mask image. The unsharp mask is then subtracted from the original image according to the equation:

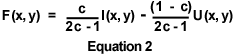
In Equation 2, the function F(x, y) represents the brightness value of a pixel at the coordinate (x, y) in the filtered image, and I(x, y) and U(x, y) represent the brightness values of the corresponding pixels in the original and unsharp mask (blurred) images, respectively. The constant c controls the relative weightings of the original and blurred images in the difference equation. In the tutorial, the Weighting Value slider can be used to control the value of c within the range of 1 (the zero percent position), to 5/9 (0.556) at the 400 percent filtering level. Similarly, the Standard Deviation slider determines the standard deviation (measured in pixels) of the Gaussian function utilized to generate the kernel mask.

The equation presented above (Equation 2) demonstrates that an unsharp mask filter operates by subtracting appropriately weighted parts of the unsharp mask from the original image. Such a subtraction operation enhances high-frequency spatial detail at the expense (attenuation) of low-frequency spatial information in the image. This occurs because high-frequency spatial detail removed from the unsharp mask by the Gaussian filter is not subtracted from the original image. In addition, low-frequency spatial detail that is passed by the Gaussian filter (to the unsharp mask) is almost entirely subtracted from the original image. This explains why increasing the size of the Gaussian filter mask usually causes the unsharp mask filter to produce a sharper image.

One of the primary advantages of the unsharp mask filter over other sharpening filters is the flexibility of control, because a majority of the other filters do not provide any user-adjustable parameters. Like other sharpening filters, the unsharp mask filter enhances edges and fine detail in a digital image. Because sharpening filters also suppress low frequency detail, these filters can be used to correct shading distortion throughout an image that is commonly manifested in the form of slowly varying background intensities. Unfortunately, sharpening filters also have the undesirable side effect of increasing noise in the filtered image. For this reason, the unsharp mask filter should be used conservatively, and a reasonable balance should always be sought between the enhancement of detail and the propagation of noise.

---

BACK TO DIGITAL IMAGE CAPTURE AND PROCESSING

BACK TO THE OLYMPUS MIC-D DIGITAL MICROSCOPE

Questions or comments? Send us an email.

© 1995-2022 by Michael W. Davidson and The Florida State University. All Rights Reserved. No images, graphics, software, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners.

This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the
National High Magnetic Field Laboratory.

Last Modification Wednesday, Jan 11, 2017 at 11:01 AM

Access Count Since September 17, 2002: 15509

Visit the website of our partner in introductory microscopy education: