Polarized Light Microscopy
Interactive Java Tutorials
Brewster's Angle
Light that is reflected from the flat surface of a dielectric (or insulating) material is often partially polarized, with the electric vectors of the reflected light vibrating in a plane that is parallel to the surface of the material. Common examples of surfaces that reflect polarized light are undisturbed water, glass, sheet plastics, and highways. In these instances, light waves that have the electric field vectors parallel to the surface are reflected to a greater degree than those with different orientations. This tutorial demonstrates the polarization effect on light reflected at a specific angle (the Brewster angle) from a transparent medium.
The tutorial initializes with an incident light ray having a pre-selected wavelength (426 nanometers) impacting the surface of a rectangular dielectric medium of specific refractive index. To operate the tutorial, use the Refractive Index slider to vary the value between 1.0 and 3.0. As this slider is translated, the incident light wave angle changes to maintain the correct Brewster angle for reflection of polarized light. The Wavelength slider can be utilized to adjust the wavelength of the incident light wave. Although varying the wavelength has no bearing on the Brewster angle calculations, it may help improve contrast to allow easier viewing of the tutorial. Moving the View Angle slider rotates the rectangular medium orientation to give different perspective views of the phenomenon.
The optical properties of the insulating surface determine the exact amount of reflected light that is polarized. Mirrors are not good polarizers, although a wide spectrum of transparent materials act as very good polarizers, but only if the incident light angle is oriented within certain limits. An important property of reflected polarized light is that the degree of polarization is dependent upon the incident angle of the light, with the increasing amounts of polarization being observed for decreasing incident angles.
When considering the incidence of non-polarized light on a flat insulating surface, there is a unique angle at which the reflected light waves are all polarized into a single plane. This angle is commonly referred to as Brewster's angle, and can be easily calculated utilizing the following equation for a beam of light traveling through air:
where n is the refractive index of the medium from which the light is reflected, q(i) is the angle of incidence, and q(r) is the angle of refraction. By examining the equation, it becomes obvious that the refractive index of an unknown specimen can be determined by the Brewster angle. This feature is particularly useful in the case of opaque materials that have high absorption coefficients for transmitted light, rendering the usual Snell's Law formula inapplicable. Determining the amount of polarization through reflection techniques also eases the search for the polarizing axis on a sheet of polarizing film that is not marked.
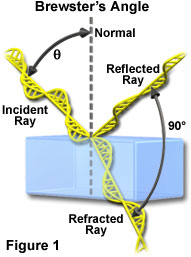
The principle behind Brewster's angle is illustrated Figure 3 for a single ray of light reflecting from the flat surface of a transparent medium having a higher refractive index than air. The incident ray is drawn with only two electric vector vibration planes, but is intended to represent light having vibrations in all planes perpendicular to the direction of propagation. When the beam arrives on the surface at a critical angle (Brewster's angle; represented by the variable q in Figure 3), the polarization degree of the reflected beam is 100 percent, with the orientation of the electric vectors lying perpendicular to the plane of incidence and parallel to the reflected surface. The incidence plane is defined by the incident, refracted, and reflected waves. The refracted ray is oriented at a 90-degree angle from the reflected ray and is only partially polarized.
For water (refractive index of 1.333), glass (refractive index of 1.515), and diamond (refractive index of 2.417), the critical (Brewster) angles are 53, 57, and 67.5 degrees, respectively. Light reflected from a highway surface at the Brewster angle often produces annoying and distracting glare, which can be demonstrated quite easily by viewing the distant part of a highway or the surface of a swimming pool on a hot, sunny day. Modern lasers commonly take advantage of Brewster's angle to produce linearly polarized light from reflections at the mirrored surfaces positioned near the ends of the laser cavity.
Contributing Authors
Mortimer Abramowitz - Olympus America, Inc., Two Corporate Center Drive., Melville, New York, 11747.
John C. Long, Matthew J. Parry-Hill, and Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
