The Fresnel, or refractive index, ellipsoid describes the dielectric properties measured in all directions through a material. Measurements through the radius yields the refractive index (n) or the square root of the dielectric constant for waves whose electric displacement vectors lie in the direction of the ellipsoid radius. This tutorial explores variations in the shape and dimensions of the ellipsoid as a function of refractive index.

The tutorial initializes with a prolate ellipsoid appearing in the window that represents an optically positive birefringent crystal. The z axis is considered the optic axis in this model, which can be rotated in three dimensions by clicking and dragging with the computer mouse. A cross section is drawn through the ellipse, which yields the refractive index ellipse (see below) for waves traveling normal to that section. The major and minor axes of the ellipse denote the refractive indices encountered by the slow and fast waves, and are adjustable with the Refractive Index sliders in the tutorial window.

The dielectric constant is anisotropic in many substances. Take a cube of such a substance and place it on a Cartesian coordinate, with the sides of the cube parallel to the x, y, and z axes. The dielectric constant for an electric field measured along the x axis—that is, x measured by placing the plates of a capacitor on the faces of the cube parallel to the y-z plane (the plane that contains the y and z axes, or that is perpendicular to the x axis)—would have one value, x(x). Along the y axis, it would have another value, x(y), and along the z axis, a third value, x(z).

The square roots of these three dielectric constants are now taken and made the length of the x, y, and z axes, proportional to these values. An ellipsoid (known as the Fresnel ellipsoid) is then drawn that has radii coinciding with the x, y, and z axes as just defined (Figure 1). The Fresnel ellipsoid describes the dielectric properties of a material when they are measured in all directions. Each radius provides the dielectric constant square root value for an electromagnetic wave that has an electric vector laying in the direction of that radius.

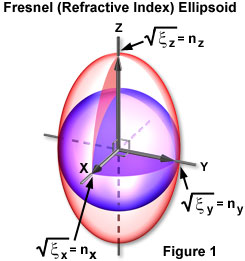
Presented in Figure 1 is a diagrammatic illustration of a refractive index, or Fresnel, ellipsoid. The radius of the ellipsoid yields the refractive index (n), or the square root of the dielectric constant for waves whose electric displacement vectors lie in the direction of the radius of the ellipsoid within an anisotropic medium. A cross section through the center of the ellipsoid produces a refractive index ellipse for waves traveling normal to that section. The major and minor axes of the ellipse denote the refractive indices encountered by the slow and fast waves, which vibrate with their electric displacement vectors along those two axes.

Because the square root of the dielectric constant equals the refractive index, the Fresnel ellipsoid is in fact a refractive index ellipsoid. As illustrated in Figure 1, the square root of the x-component dielectric constant represents the refractive index for electromagnetic waves whose electric field vectors are vibrating in the x-axis direction. It also follows that the square root of the dielectric constant for the y and z components corresponds to waves with electric fields vibrating along the y and z axes, respectively.

The value of the refractive index given by the radius of the Fresnel ellipsoid is valid for all waves with an electric vector that vibrates in the direction of that radius, regardless of the wave's direction of propagation. For example, waves with their electric vector in the x-axis direction may be propagating along the y-axis or z-axis. Therefore, given the direction of the electric vector (or more properly, the electric displacement vector in the material medium), the refractive index suffered by a wave is defined regardless of its direction of propagation.

The Fresnel ellipsoid is used to obtain an index ellipse by cutting a cross-section of the three-dimensional ellipsoid perpendicular to the direction of light propagation. For light traveling in any direction, the index ellipse is obtained by making a major cross section of the ellipsoidal perpendicular to that direction of travel. The index ellipse yields the refractive indices and indicates the vibration direction (of the electric vector) of the light waves, because the waves vibrate with the electric vectors along the major and minor axes of the index ellipse. The refractive indices that the two waves experience are given by the major and minor radii of the ellipse. In other words, for each direction of travel in an anisotropic medium, there are two plane-polarized light waves that vibrate perpendicular to each other and travel at different velocities. This is, in fact, the phenomenon of birefringence.

---

BACK TO OPTICAL BIREFRINGENCE

BACK TO POLARIZED LIGHT MICROSCOPY

Questions or comments? Send us an email.

© 1998-2022 by Michael W. Davidson and The Florida State University. All Rights Reserved. No images, graphics, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners.

This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the
National High Magnetic Field Laboratory.

Last modification: Monday, Sep 18, 2017 at 11:04 AM

Access Count Since April 25, 2001: 93246

For more information on microscope manufacturers,
use the buttons below to navigate to their websites: