The binary images produced by thresholding rarely provide a perfect delineation of the features or structures of interest. Variations in pixel brightness or color, such as random or shot noise in the original image, can cause some pixels to be included or excluded. Imperfections introduced in specimen preparation or imaging can include fine lines or rough borders. These types of defects in binary images are usually addressed by morphological operations.

The basic morphological functions are erosion, the removal of pixels from the periphery of a feature, or dilation, the adding of pixels to that periphery. Classical erosion removes any pixel that has a background neighbor (any of the eight neighbors that share an edge or corner). Conversely, classical dilation adds any pixel that touches a pixel in the feature. Of course, both of these operations change the size of features or structures and so they are most often used together. An opening is an erosion followed by a dilation, while a closing is a dilation followed by an erosion. These operations can smooth irregular borders, and fill in or remove isolated pixel noise and fine lines.

In the Iterative Morphological Operations interactive tutorial, each function can be applied multiple times to add or remove more pixels. An opening of M iterations consists of M steps of erosion, followed by M steps of dilation, and vice versa.

A greater degree of control over the types of defects that are corrected is obtained by replacing the classical erosion rules with conditional ones. For example, instead of erosion removing a pixel that touches any background pixel, the conditional rule removes it only if it touches more than N background pixels (where N can range from 0 - the classical case - to 7). With this modification, it becomes possible to selectively add or remove isolated pixels or fine lines without affecting larger structures.

	Interactive Tutorial
Iterative Morphological Operations Perform erosion, dilation, opening, or closing on a binary image with single or multiple iterations and adjustable neighborhood conditions.

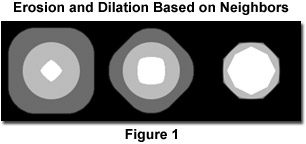
Erosion and dilation based on neighbor comparisons work well for small defects, when no more than 1 or 2 iterations are required. But important limitations arise with larger numbers of iterations: the results are anisotropic because pixels are that are added or removed have greater dimensions in the diagonal directions, and the distances affected vary with direction and with the conditional neighbor test. Figure 1 shows a circle and the results of applying 25 iterations of erosion (white) and dilation (dark gray) using conditional neighbor tests of 0 (classical morphology), 1, and 3.

More isotropic and also faster application of erosion and dilation is possible using the Euclidean distance map (EDM). This function assigns gray values to each feature pixel in a binary image with a value that corresponds to the distance from that pixel to the nearest background pixel. Thresholding the EDM of the feature produces erosion, while thresholding the EDM of the background produces dilation, as shown in the EDM-Based Morphological Operations interactive tutorial. The distance can be adjusted accurately and the results retain feature shapes as shown in Figure 2. The EDM of the circle is shown in the center of the diagram, and the result of erosion and dilation by 25 pixels at the right. However, the conditional iterative morphological tools are also useful because of their ability to select isolated points and lines.

	Interactive Tutorial
EDM-Based Morphological Operations Perform erosion, dilation, opening, or closing on a binary image using the Euclidean Distance Map (EDM).

---

BACK TO INTRODUCTION TO DIGITAL IMAGE PROCESSING AND ANALYSIS

BACK TO MICROSCOPY PRIMER HOME

Questions or comments? Send us an email.

© 1998-2009 by Michael W. Davidson, John Russ, Olympus America Inc., and The Florida State University. All Rights Reserved. No images, graphics, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners.

This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the
National High Magnetic Field Laboratory.

Last modification: Tuesday, Sep 11, 2018 at 01:27 PM

Access Count Since July 20, 2006: 17560

For more information on microscope manufacturers,
use the buttons below to navigate to their websites: