Willebrord Snell was an early seventeenth century Dutch mathematician who is best known for determining that transparent materials have different indices of refraction depending upon their composition. Snell was born to an affluent family in Leiden in 1580, and started studying mathematics as a very young man. His father was a scholar and professor of mathematics at the University of Leiden.

Snell entered the University of Leiden at a relatively young age where he originally studied law. His attention soon turned to mathematics and he was teaching at the university by the time he was 20 years old. After finishing with his degree at the university, he traveled to eastern Europe and visited most of the major astronomers of the day.

In 1613, Snell succeeded his father as professor of mathematics at Leiden and in 1617, he published Eratosthenes Batavus, which explained his methodology for measuring the Earth by triangulation. Snell had difficulty completing his work until the brother barons Sterrenberg took over and finished it with his assistance. This important work wove the foundations of modern geodesy.

Snell also published other works, including his work on comets and in 1624, he published Tiphys Batavus, a work on navigational theories. His work in mathematics allowed him to produce an improved method of calculating approximate values of pi using polygons. This method, using 96-sided polygons, produce a value of pi correct to seven places, a striking improvement to the classical method that yielded only two places.

The laws of refraction of light remain Snell's most important contribution to science, although they were not published until almost 70 years after his death. The Egyptian geographer Ptolemy initiated the study of refraction and described a law to explain the degree of diffraction even though his results did not always agree with his law. Ptolemy was followed by Arab scientist Alhazen, who also studied refraction, but could not predict how far light would bend when entering a medium of greater refractive index.

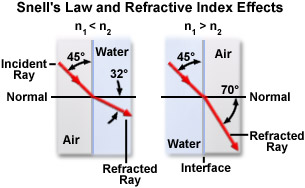
Snell discovered that a beam of light would bend as it enters a block of glass, and that the angle of bending was dependent upon the incident angle of the light beam. Light traveling in a straight line into the glass will not bend but, at an angle, the light is bent to a degree proportional to the angle of inclination. In 1621, Snell found a characteristic ratio between the angle of incidence and the angle of refraction. Snell's law demonstrates that every substance has a specific bending ratio—the "refractive index. The greater the angle of refraction, the higher the refractive index for a substance.

Snell's Law can be described as follows:

Where n represents the refractive indices of material 1 and material 2 and q are the angles of light traveling through these materials with respect to the normal. There are several important points that can be drawn from this equation. When n(1) is greater than n(2), the angle of refraction is always smaller than the angle of incidence. Alternatively when n(2) is greater than n(1) the angle of refraction is always greater than the angle of incidence. When the two refractive indices are equal (n(1) = n(2)), then the light is passed through without refraction.

Snell died at the relatively young age of 46 on October 30, 1626 in Leiden. He would never realize how the importance of his discovery of the basic laws of refraction would prominently position his name in textbooks on physics and optics.

BACK TO PIONEERS IN OPTICS

Questions or comments? Send us an email.

© 1995-2022 by Michael W. Davidson and The Florida State University. All Rights Reserved. No images, graphics, software, scripts, or applets may be reproduced or used in any manner without permission from the copyright holders. Use of this website means you agree to all of the Legal Terms and Conditions set forth by the owners.

This website is maintained by our
Graphics & Web Programming Team
in collaboration with Optical Microscopy at the
National High Magnetic Field Laboratory.

Last Modification Friday, Nov 13, 2015 at 01:19 PM

Access Count Since December 24, 1999: 106176

Visit the websites of our partners in education: